Thermal Bridging

Background

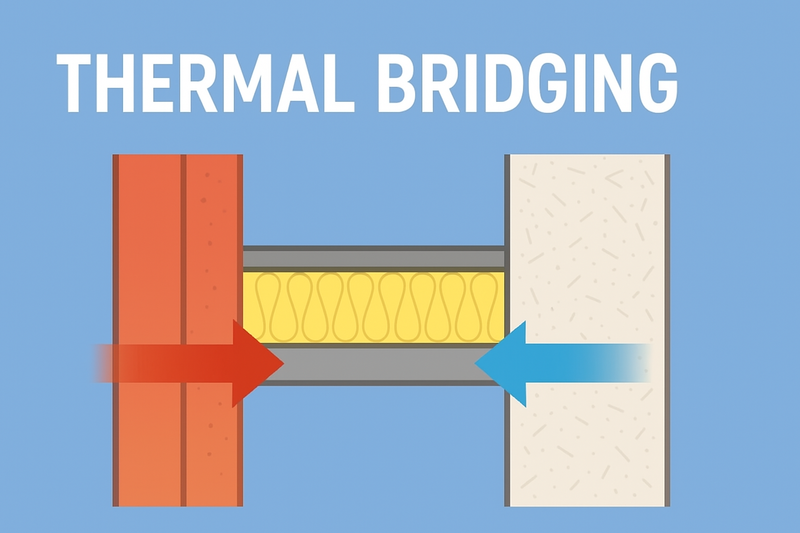
The effect of thermal bridging is important when performing a full-year energy analysis on a building envelope, yet it is often not considered during load calculations, despite the fact that it can have a noticeable effect on insulation performance.

“Thermal bridging” is the term used to describe when a highly thermally conductive material creates an alternate path of heat transfer, essentially creating a “bridge” for heat to move across from one side to another. When this occurs, the effect of insulation is no longer as relevant, and any incremental improvement in insulation has a lower impact than it would otherwise have. The classic example is a wall with a cavity for insulation and studs that are located at regular intervals in the cavity. The studs can easily be 5x as conductive as the insulation, allowing heat to move from one side of the wall to the other, using the stud as a bridge.

Calculations

Calculating the effects of a thermal bridge is similar to calculating current flow through parallel circuitry. Where heat is travelling through the thermal bridge as well as the regular wall assembly simultaneously, the equation to calculate net resistance is

$R_{net}=\frac{1}{\frac{1}{R_b}+\frac{1}{R_w}}$

Where R_b is the thermal resistance of the bridge and R_w is the resistance of the wall, in units of $\frac{^oF}{Btu/h}$. If the thermal bridges are regularly occurring, such as studs occurring in a wall every 16” on centers, then we can take a sample piece of the wall to calculate the net effect of the studs.

For example, suppose a wall assembly has an insulation cavity that is 3.5” thick with batt insulation and oak studs that are 1.5” thick, located every 16”. Since any 16” piece of wall length will include exactly one full stud, then we can take any sample of 16” for consideration.

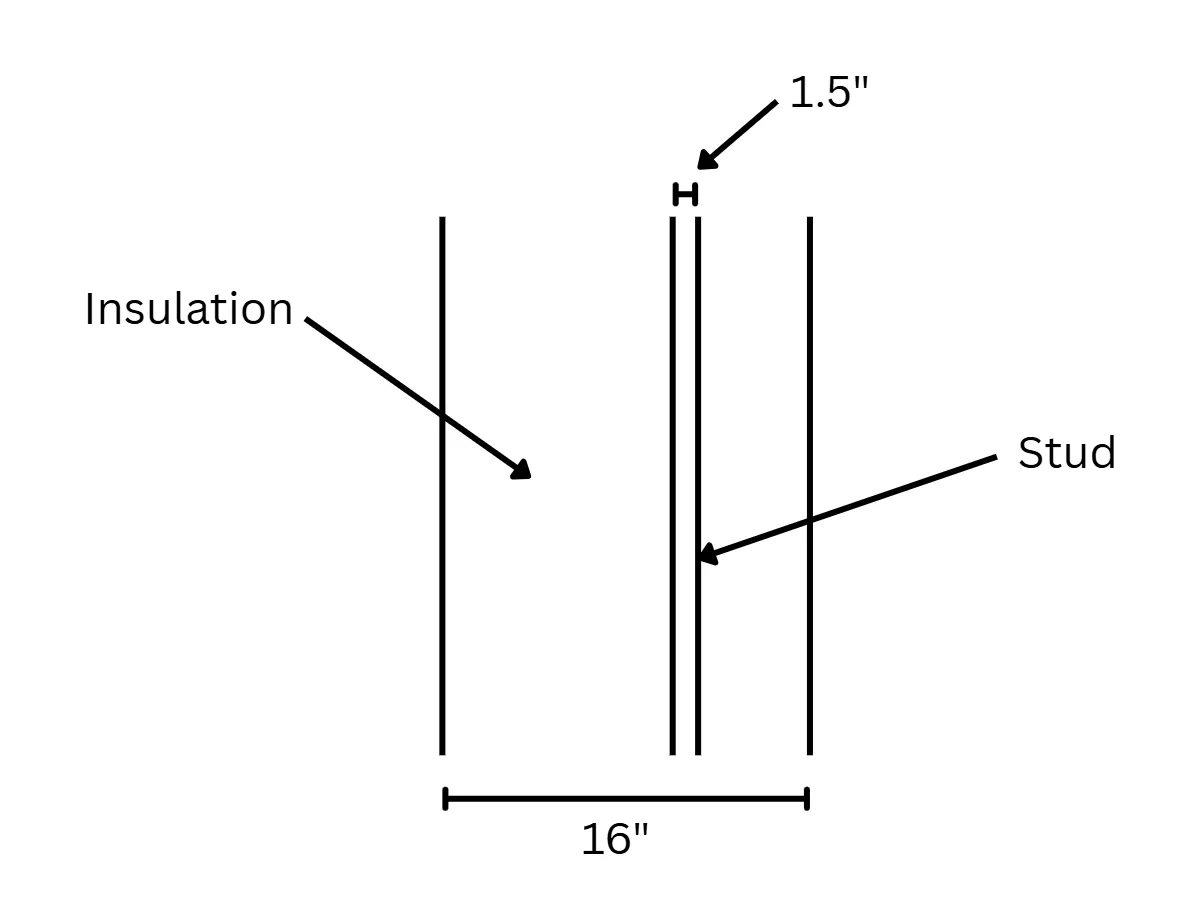
We therefore have 14.5” of insulation and 1.5” of wood stud for the total height of the wall. In a 3.5” thick wall cavity, batt insulation has an R’-value of approximately 15.2 $\frac{^oF ft^2}{Btu/h}$, and an oak stud has an R’-value of approximately 1.94 $\frac{^oF ft^2}{Btu/h}$, where R’ means the area-adjusted R-value (notice the adjustment to the units). Keep in mind the important equation

$R=\frac{1}{U\times A}$

Where U=1/R’ is the heat transfer coefficient in $\frac{Btu/h}{^oF ft^2}$ and A is the area. We can then adjust the area accordingly for each R-value in this example

$R_{ins}=\frac{1}{U_{ins}A_{ins}}$

$R_{stud}=\frac{1}{U_{stud}A_{stud}}$

Since the areas are normalized to 1’ of height, we can simply use the relative widths of each section, setting $A_{ins}=14.5/16$ and $A_{ins}=1.5/16$. Now solving each R-value yields

$R_{ins}=\frac{1}{(1/15.2)(14.5/16)}=16.77 \frac{^oF\space ft^2}{Btu/h}$

$R_{stud}=\frac{1}{(1/1.94)(1.5/16)}=20.69 \frac{^oF\space ft^2}{Btu/h}$

Notice that the units still include $ft^2$ in the numerator even though these were calculated as R-values instead of R’-values. That is because the area was normalized to 1’ of height and an average per 16” of width. This allows us to make the final calculation step still under normalized numbers by using the parallel resistance equation

$R_{net}=\frac{1}{\frac{1}{16.77}+\frac{1}{20.69}}=9.26 \frac{^oF\space ft^2}{Btu/h}$

Since the units of $ft^2$ are still here, it means this is in fact an R’-value, which means to use it in an equation, it would come in the form of the equation $q=\frac{A\Delta T}{R_{net}}$ where A is the area and $\Delta T$ is the temperature differential across the wall.

The point of this example is to show the magnitude of the effect of simply adding a highly conductive bridge through the insulation. This brought the R’ value from 15.2 to 9.26, a reduction in thermal resistance of 39%, despite the fact that the stud only occupies 9.4% of the wall area. As insulation increases, the impacts diminish in value due to the fact that all heat transfer starts moving toward the stud. Even if we doubled the insulation R’-value from 15.2 to 30.4, our net R’-value becomes 12.80 - a 58% decrease from just the plain insulation resistance of 30.4.

Conclusion

While most building codes for commercial buildings address the issue of thermal bridging, it still needs to be analysed and addressed by the building design team. This example was about studs in wall cavities, but thermal bridging can come in many other forms, such as window frames, balconies, or pins holding insulation to drywall. This example shows that properly analysing the effect of thermal bridging can be an important piece of properly modelling the performance of a building, and understanding where thermal bridging is likely to occur is one of the keys to designing energy efficient buildings.